Why Is There A Minus 1 In the Annuity Formula


I was learning about the annuity formula in a math class I was taking. 

Math and formulas are fun and really cool. Formulas, especially, are cool because they allow you to do complicated, time-consuming things much more quickly than you could without them. 

I am a nerd and I love that moment when I fully understand a formula and how it came to be, the proof of the formula. 

But I was struggling to understand the Annuity Formula. Much of it made sense. It is basically just compounding interest applied to many equal payments over time, and then summing the payments and various amounts of interest accrued over time. 

But I didn’t understand the -1 (minus one) part of the equation. 

The equation looks like this:

Annuity Formula


Here are the variable declarations.
A = the final value of all investment and accrued interest
m = the amount of each annuity payment
r = the annual interest rate
n = the number of times per year that payments are made
t = time, in years, over which the investment spans

So all of it makes sense. 

The formula is based on the general “Sum of a Geometric Series” formula. In the “Sum of a Geometric Series”, each consecutive term is connected by a common ratio. Each term gets the next term in the series when multiplied by the same amount (which is different from the “Sum of an Arithmetic Series” in which each term gets the next by adding or subtracting the same amount). 

The 
Compound Interest Formula
part is just the compound interest formula. 

I just couldn’t figure out why there was the -1 in the numerator. 

I searched Google and Youtube for an explanation video which would prove the equation, and luckily, I found one that cleared everything up for me.

Annuity Formula Proof Video

What I realized after I watched the video was that in an ordinary annuity, payments are made at the end of each month. That means that for month number 0, there is no payment and no accrued interest. 

The equation is based on numbers on a number line, and the number line has to start at zero, but since nothing happens until the end of that month a minus one subtracts that month. 

That is where I was getting hung up. 

I hope that this clarification helps you to understand and apply this very excellent formula.



Other Articles to Read

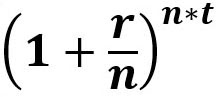
Comments

Post a Comment

Popular posts from this blog

What Is the Purpose of a Blog Post?

Image
When people are new to blogging and they are trying to research what makes a good blog post or how to improve their blog’s performance measures through their content, a certain type of advice comes up almost every time. “Write the BEST content on your article’s topic.” “Make your article better than every other article on the web.” “Make your post the definitive, most detailed resource available.” “If someone finds your article, they shouldn’t need to look for any other information anywhere else because your post will be so complete that they will have learned all they need to learn about the subject.” This is a wildly intimidating goal to set for your content, and unfortunately, while the intention of setting a lofty goal is that you will end up achieving better results for it, what most often happens is that you will develop a fear of failure and that will prevent you from even starting. Which is the worst possible outcome. Even a failure that gets finishe
Read more

The Importance of Entrepreneurship to the Economy and Society

Image
An entrepreneur is a special kind of person.  The entrepreneur is a life/world/reality designer.  The entrepreneur takes what isn’t yet and makes it happen. Someone who is entrepreneurial or chooses the path of entrepreneurship will create the world that others live in.  Where most people must settle for the way things are and must pounce on the job opportunities they see in the world because those are the limit of possibilities for them, the entrepreneur will choose to create opportunities for themselves and others when they do not see the opportunities they wish for. Clearly, I think highly of entrepreneurs. Can Everyone Be An Entrepreneur? I think that there are some people who lack the skills and the mindset to ever be entrepreneurial. They will go through their entire life only taking what other people give to them or allow them the chance to work for. All of their life’s choices are simply what more spirited people have created for them. 
Read more

Can Blogger Blogspot Blogs Rank In Google?

 I am a blogger. I want to write articles about things I care about, have them crawled, indexed, and ranked by search engines, and have people organically find and read my content. I am not writing only for me (although I do enjoy the process of blogging and writing my ideas out), I am writing to attract and inform/entertain an audience. If my content does not rank in the search engines, then nobody will find my content, and there is much less of an incentive for me to be blogging. From Google's perspective (and the other search engines), it seems that they want to show users the best possible content which will satisfy their queries. They should not have any biases for or against any sort of content. So long as a piece of content is valuable to readers, it should show up in the results. That is just good business for them. With the millions of blog posts being published every day , it is very difficult for a company like Google to determine which articles are the best quality and
Read more